Enhancing Depth of Focus with Negative Spherical Aberrations: From Theory to Clinical Impact
The introduction of optical aberrations has become a prevalent approach in refractive and cataract surgery to enhance the depth of focus, compensating for the loss of accommodation associated with presbyopia. Negative spherical aberration (NSA), in particular, is widely employed in procedures like presbyLASIK and Extended Depth of Focus (EDOF) intraocular lenses (IOLs), where controlled induction of spherical aberration plays a key role. This page seeks to provide a refresher on the mechanisms involved in using negative spherical aberration and to clarify the conditions essential for its successful application—conditions that are often overlooked or even (deliberately?) obscured.
Core Concepts
The notion of optical aberration is as intuitive as it is abstract. In geometric optics, where the focus is on image location, size, and potential distortion, light is often represented as rays converging at a focal point. A wavefront is a virtual construction: it corresponds to the envelope of points in space that share the same phase, with variations represented by wave trains (sinusoids). A ray is another virtual construct that represents the local direction of the wavefront’s movement.
Vergence is a quantity expressed in Diopters, which is equal to the inverse of a distance. It is the refractive index of the propagation medium divided by the distance from (negative vergence) or towards (positive vergence) the focus. Thus, the farther from the source, the lower the vergence (in absolute value). If the source is at a great distance or infinity, the vergence incident on an optical element (diopter, lens) is zero. Vergence is a familiar concept for clinicians; reading a book requires a vergence of approximately 3 D (for a book positioned about 35 cm from the eye).
Rays represent the local propagation of the wavefront, which itself represents the envelope of points in the same phase state. In wave optics, the concepts of optical path and corresponding phase shift prevail. The distance between a wavefront and its focal point allows for the calculation of vergence, which involves its reciprocal and the refractive index of the medium considered.
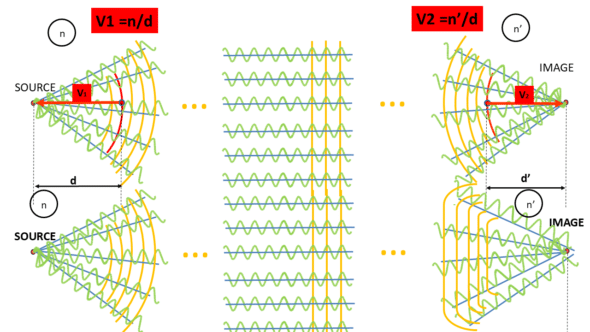
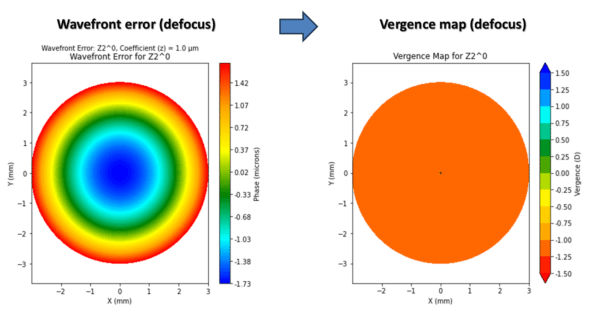
Consider a point source emitting light in all directions. We represent only part of the emitted light here in the form of wave trains, rays, and wavefronts, though our considerations will involve vergence. An optical system designed to converge light to a focal point can form an image of the point source from a portion of the captured wave/ray trains. Vergence is a paraxial concept, at least when using the vergence formula, though it can be extended to the wavefront envelope for didactic purposes. When the system is free of optical aberrations (top), vergence is the same for all points on a wavefront. In the presence of aberrations (bottom), the wavefront distortion causes vergence to vary at different points, as the envelope is no longer spherical (parabolic in the first approximation), and the physical distance of envelope points to the paraxial focus varies – These diagrams are not to scale.
Aberrations and their classifications aim to model and rationalize situations where there is an optical path difference between light from a source and the image plane, relative to an ideal optical system. The optical path concept naturally leads to phase difference and wavefront error surfaces.
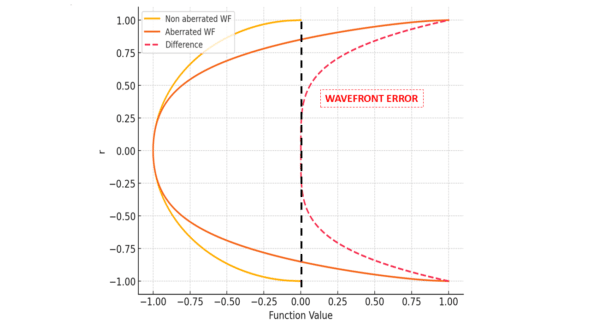
The study of the wavefront concerns the differences between the measured wavefront (with aberrations) and the ideal wavefront (reference). In this example, the difference is a pure fourth-degree spherical aberration. (the normalized pupil radius is plotted on the Y-axis)
As we will see, these optical path differences (in wavelength) or phase changes can also be translated into local power (vergence) variations, providing insight into the refractive impact of spherical aberrations.
For clarification, negative spherical aberration (NSA) in this context is measured in a setup where light rays emanate from a distant source (i.e., for “distance vision”).
Ray Tracing Representations of Negative Spherical Aberration
A simple way to represent NSA is through ray tracing in a biconvex symmetrical aspheric lens having two highly prolate surfaces.
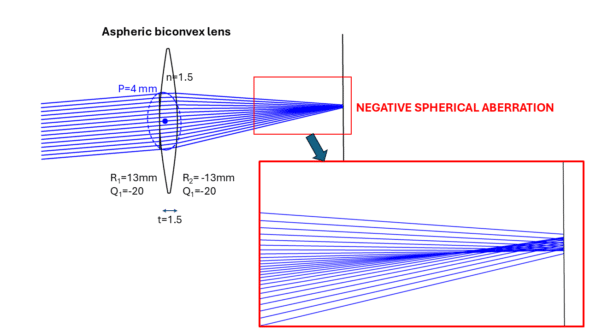
Biconvex lens with hyperprolate surfaces, generating negative spherical aberration. The enlarged detail reveals an area of light concentration (caustic). The image plane has been shifted away from the « best foci zone » to visualize the caustic better.
With NSA, paraxial rays—those close to the optical axis—converge first, forming a proximal focal point zone. In contrast, rays farther from the axis are refracted at a greater distance, creating a pattern called « a caustic. » This pattern indicates an area where light is concentrated enough to form an interpretable image of sufficient quality in a plane that would intersect the caustic.
NSA fundamentally represents a gradual focal length increase for peripheral rays, illustrating a consistent defocusing progression as rays become more peripheral.
Through focus spot diagrams are valuable tools for visualizing how an optical system focuses light from different field angles or object distances. By plotting the distribution of light spots on a focal plane, these diagrams reveal the presence and impact of optical aberrations, such as spherical aberration:
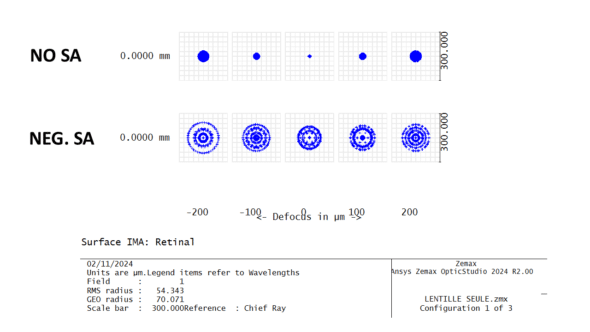
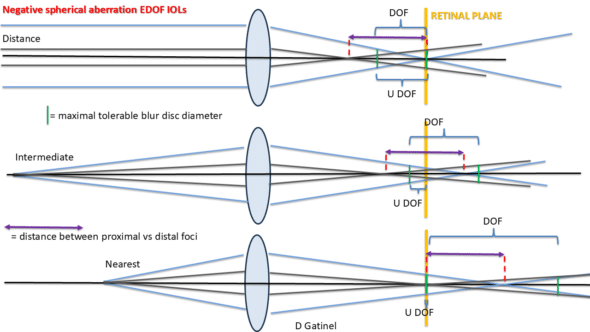
Comparison between a lens corrected for spherical aberration and a lens with negative spherical aberration. Optical performance is reduced in the latter case but remains relatively stable across different defocus values. The effective depth of field depends on the maximum tolerable blur spot diameter and the position of the focal points within the interval where blur remains below this diameter. Ideally, these points should be located in front of the retinal plane for rays originating from a distant source—or behind it for rays from the nearest target that still appears sufficiently clear.
A “functional” representation of NSA would be beneficial in clinical applications aimed at providing sufficient vision across various distances for presbyopic eyes. It is ideal for variable distance-situated sources to yield a sufficiently concentrated image plane (retinal) focus.
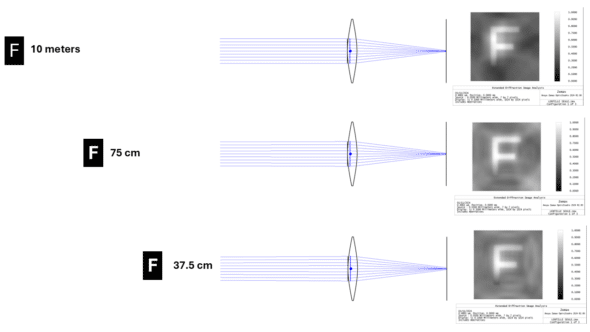
Simulations for different target distances with the previous Negative spherical aberrated lens. The letter is identifiable despite the overall reduction in contrast that is already noticeable for the distant target (10 meters). Interestingly, the rays that help preserve detail for the image of the target from a distance are refracted at a distance from the optical axis. The closer the targets are, the closer the rays are focused in the image plane to the optical axis.
Importantly, NSA alone does not extend the depth of focus in an emmetropic eye (in which paraxial rays are focused in the retinal plane) and can degrade optical quality without improving near vision at all! Indeed, if paraxial rays from a distant source produce emmetropia, non-paraxial rays will be defocused onto a plane located behind the retina. This will inevitably be the case for all rays from nearby sources, as they will have a divergent incidence!
Conversely, if rays refracted paracentrally by a nearby target are conjugate with the retina, this refraction can, by definition of myopia (punctum remotum located at finite distance), be considered myopic. In this configuration, the superimposition of these paracentral rays, defocused in front of the retina, with less paracentral rays gradually focused on the retinal plane should allow for sufficiently clear distance vision (controlling the induced blur).
Seidel’s Classification and Spherical Aberration
Seidel’s classification is simple but effective, defining spherical aberration as:
W(r) = a40 ⋅ r4
a40 is a weighting coefficient. This function describes the wavefront deviation due to spherical aberration. For negative SA : a40 < 0
The r4 term designates spherical aberration as a fourth-order aberration. This wavefront error map reflects the gradual defocus of rays as they are refracted further from the optical axis.
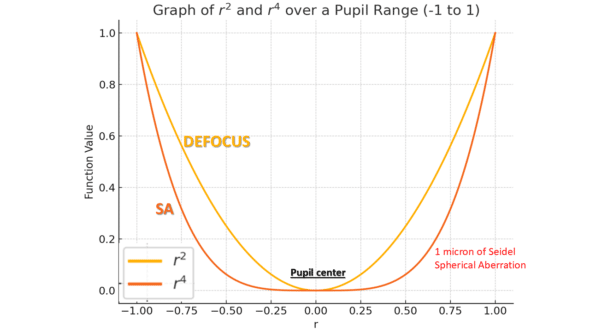
Spherical aberration is a wavefront error of the fourth order (radial degree 4). This wavefront error primarily affects the edge of the pupil, unlike defocus aberration (degree 2), which impacts the entire pupil area. For a small pupil diameter, the expected impact of Seidel-type spherical aberration on subjective refraction is negligible. Towards the pupil edges, the effect of spherical aberration adds to that of defocus if they share the same sign. If defocus is positive (indicating myopia, by convention) and the spherical aberration is also positive, myopia increases at the pupil periphery. In this case, vergence is no longer uniform across the pupil. Conversely, if defocus is negative (indicating hyperopia) and spherical aberration is negative, the hyperopic defocus intensifies towards the edges.
The wavefront error due to NSA increases slowly initially, accelerating at the pupil’s edge, a hallmark of high-order aberrations in ophthalmology. Although Seidel-like NSA’s effect on refractive error is limited—particularly since central rays largely determine clinical refraction—the peripheral defocusing typical of an emmetropic eye can reduce retinal image quality (contrast) by shifting peripheral ray focus behind the retina.
Zernike Spherical Aberration
The representation of spherical aberration in the Zernike classification is more complex, if not problematic. This is due to reasons that we won’t elaborate on here but which relate to the need for these functions to possess certain mathematical properties that, while desirable in instrumental optics, are less suitable in clinical ophthalmology. Put bluntly, the representation of negative spherical aberration in the Zernike classification undermines the very principle of effectively segregating aberrations that can be corrected with glasses (second-degree) from those that cannot (fourth-degree).
The Zernike polynomial Z40 with normalization coefficient is:
Z40(r) = √5 * (6r4 – 6r2 + 1)
Where:
- r is the normalized radial coordinate (0 ≤ r ≤ 1).
- The coefficient √5 is the normalization factor.
One need only compare the wavefront error equation with that of the Seidel classification to observe an oddity. Here, NSA is expressed with a second-order term (defocus) opposite in sign to the primary fourth-order term. There is also a constant term, which has no impact on the optical plane and exists solely due to analytical constraints that are largely irrelevant in a clinical context.
This helps explain why the Zernike fourth-degree spherical aberration takes on this “sombrero” shape: the central bulge corresponds to the influence of the second-degree term, dominating at the center over the fourth-degree term, which only prevails from outside the outer third of the pupil diameter.
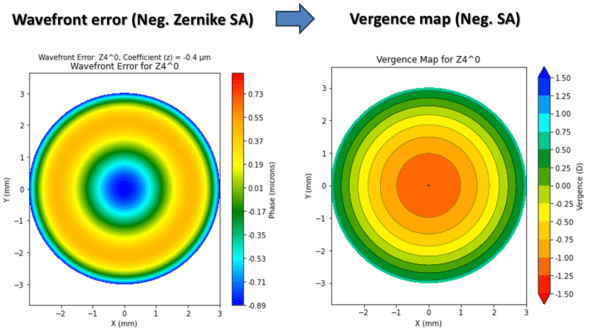
The presence of this defocus term is far from incidental—quite the opposite. A simple analytical study shows that for a coefficient z40 of 1 micron of Zernike spherical aberration, there are over 4 microns of associated defocus of the opposite sign! The impact of defocus within that Zernike mode is naturally proportional to the coefficient that scales it. In the context of presbyopia compensation, where this coefficient is deliberately increased to more negative values, it cannot be ignored. For 0.25 microns of negative spherical aberration with a 6 mm pupil, the amount of defocus present (about 1 micron) corresponds to at least +0.75D of positive defocus (myopia).
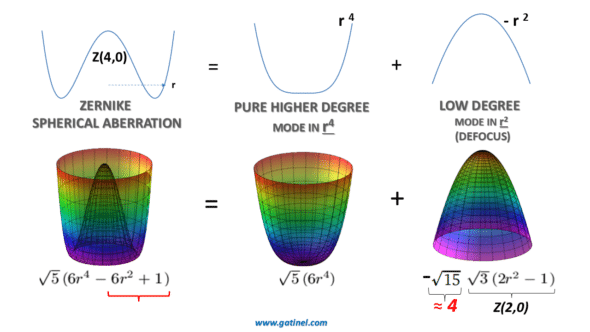
Here is represented the decomposition of the Zernike 4th order spherical aberration Z40 mode with a coefficient of 1 micron into a component in r4 and a component in r^2 …which is equivalent to roughly 4 microns of Zernike defocus Z20^!
In the Zernike convention, a negative defocus (Z20) coefficient corresponds to hyperopic refraction, and vice versa. Thus, positive spherical aberration includes a hyperopic refraction component, while negative spherical aberration includes a myopic refraction component. Subjective refraction primarily depends on the central region of the pupil, so any variation in wavefront error at this level significantly impacts the performance of the eye. Defocus leads to a marked reduction in the transmission of high spatial frequencies, which encode image detail. Achieving good uncorrected visual acuity requires a “flat” wavefront in the central pupillary region.
This blending of terms is a source of conceptual confusion and errors, which can be even more problematic as it sometimes allows certain stakeholders to exploit the resulting ambiguity to exaggerate the benefits of negative spherical aberration (NSA) and obscure some of the inherent constraints in effectively using NSA to compensate for presbyopia.
When studying the impact of Seidel-type spherical aberration on refraction, it is noted that for negative values, a slight hyperopic shift will be observed. This reflects the effect of reduced power toward the pupil periphery, even though the refraction in the paraxial zone remains unchanged. However, if Zernike negative spherical aberration is induced, the opposite effect will be seen due to the positive defocus (myopic shift) introduced by this aberration. This is a common source of confusion and can lead to partially incorrect interpretations, especially concerning Extended Depth of Focus (EDOF) implants, as highlighted in a recent letter to the editor.
To address this issue more clearly, we must return to a more clinical understanding of what high-order aberrations represent for a system’s optical properties.
Wavefront Error and Vergence Map
The concept of vergence, measured in diopters, is more familiar to ophthalmologists than optical path length or phase. However, as seen above, it is possible to link these concepts, albeit approximately, by interpreting the refractive impact of high-order aberrations on the eye’s refractive properties (expressed in diopters).
As recalled above, light rays can be thought of as representing the local propagation direction of the wavefront. A flat wavefront corresponds to parallel rays, while a spherical dome-shaped wavefront characteristic of pure defocus, converging towards a focal point at the dome’s center, represents a bundle of rays intersecting at that center. The curvature of this wavefront can reasonably be approximated by a parabola (a second-degree curve), and since all rays converge at the same point, it can be stated that they share the same vergence.
A purely parabolic wavefront error (degree 2) with a positive coefficient (1 micron, 6 mm pupil) corresponds to a constant vergence error of approximately –0.8 D (myopia) in the refractive plane. In the absence of high-order aberrations, there are no fluctuations in refraction across the pupil.
A system free from high-order aberrations can be considered to have uniform vergence (zero for an emmetropic eye, negative for a myopic eye, etc.). A clinically understandable definition of high-order aberrations would be that they cause the defocus value to fluctuate across the pupil! (low-order astigmatism is also responsible for a variation in local power from one meridian to another.)
For more complex wavefront shapes, certain mathematical tools allow the conversion of wavefront error into a vergence map.
Let us now examine the case of negative spherical aberration (NSA) and represent its vergence map.
Refractive Impact of Negative Zernike Spherical Aberration
Here, side by side is a wavefront error map exclusively showing negative spherical aberration and the corresponding vergence map (Zernike NSA coefficient of -0.2 microns over a 6 mm pupil):
Impact of a negative Zernike spherical aberration (coefficient of -0.2 microns for a 6 mm pupil) on vergence within the pupil. The central convexity in a sombrero shape, associated with defocus, induces a zone of myopic defocus reaching nearly 1D. A refractive gradient progressively reduces this myopia until it is neutralized, followed by the appearance of a peripheral ring of hyperopia.
For a Zernike NSA coefficient of -0.4 microns over a 6 mm pupil, there is a significant vergence variation, ranging from -1.25 D at the center to +0.75 D at the edges.
Impact of a negative Zernike spherical aberration (coefficient of -0.4 microns for a 6 mm pupil) on vergence within the pupil. The central convexity in a sombrero shape, associated with defocus, induces a zone of myopic defocus reaching nearly 1.50D. A refractive gradient progressively reduces this myopia until it is neutralized, followed by the appearance of a peripheral ring of hyperopia. There is a nearly 2-D of refractive gradient from the center (myopia) to the periphery (hyperopia) of the pupil.
We have uncovered a striking revelation: the induction of negative spherical aberration is far from refractively neutral; on the contrary, it introduces a significant myopic refractive shift. This shift is the direct result of the second-degree term embedded within the Zernike mode expression.
The myopic defocus within the Zernike spherical aberration with a negative coefficient plays a major role in increasing the depth of focus. Simply put, this aberration induces central myopia in the pupil, gradually reducing myopia towards the edges—and eventually even shifting to hyperopia at the periphery.
Consequences of the hybrid nature (low and high order) of Zernike spherical aberration
Suppose Negative Zernike SA was the only aberration present (no second-degree or other high-order aberrations), as in the above diagrams. Clinically, what would be observed? A slightly myopic refraction and, compared to a uniformly myopic pupil, better intermediate and distance vision due to the progressive reduction of myopia toward the pupil edges, followed by hyperopic refraction (generally undesirable, though potentially useful for very distant targets based on empirical observations).
However, this eye, let us remember, is theoretically only affected by high-order aberrations! Far from being truly emmetropic (as expected from an eye truly free of low-degree aberrations), it will be measured as slightly myopic, and several observations can be made:
1 – Intermediate and distance vision are expected to be better than diffuse myopia across the entire pupil (as in « blunt » monovision strategies).
2- Distance vision quality will necessarily be reduced compared to a paraxially emmetropic eye. The paradox and confusion here arise from the hybrid nature of some higher-order Zernike modes; if we adhere strictly to the clinical definition of high-order aberrations, this eye should be considered emmetropic, as it lacks second-degree aberration in the wavefront reconstruction (it is hidden in the Z40 mode)
3- Inducing emmetropic refraction near the pupil edges may be preferable to hyperopic refraction. This point is intriguing and merits further discussion, which will be covered in the next section.
4- Finally, it should be noted that simulating retinal images for high-order aberrations (and PSF, MTF, etc.) based on Zernike polynomials is clinically unrealistic: low-order terms included in high-order modes like spherical aberration and secondary astigmatism degrade the simulated image and related metrics. Unfortunately, this function basis is still used for such applications, and this can be particularly problematic in refractive surgery when attempting to illustrate the functional complaints of certain patients (read more here). Nevertheless, this remains the case for all aberrometers whose simulated retinal images and other derived metrics are clinically irrelevant when it comes to characterizing the impact of higher-order aberrations on vision using Zernike polynomials.
To summarize:
- For NSA to be useful, it must include central myopization of the pupil; otherwise, it reduces retinal contrast without increasing the depth of field.
- Using Zernike negative spherical aberration is a way to “covertly” induce central myopic refraction, aimed at enhancing near vision performance for presbyopic eyes. This is due to the hybrid nature of Zernike spherical aberration, which induces four times more defocus (second degree) than fourth degree!
A note on EDOF IOLs
The field of so-called EDOF (Extended Depth of Focus) intraocular lenses (IOLs) is not exempt from this ambiguity.
Most refractive EDOF implants rely on enhancing SA to extend the depth of focus. It is easy to see that the uncertainties introduced by using Zernike modes, when applied to implants, lead to significant challenges. The notion of emmetropia must be reconsidered with this type of IOL, which, to be effective, necessarily induces central myopia postoperatively.
An objective measurement of myopic refraction by an autorefractor is not an artifact for an implant that induces negative spherical aberration and effectively increases the depth of focus. This may potentially degrade distance vision quality, paradoxically more than diffractive optics do for smaller pupil diameters (i.e. in day-time conditions). Aiming for a slightly myopic refraction is sometimes even recommended for certain EDOF implants that induce a high level of negative spherical aberration. This approach ensures enhanced intermediate vision performance but inevitably compromises distance vision
A schematic diagram helps illustrate and validate these concepts:
In a system optimized with negative spherical aberration, non-paraxial rays focus on the retinal plane, while paraxial rays focus in front of the retina. This configuration extends the entire depth of focus (DOF) in front of the retina. Practically, it is expected that the best image quality for distance vision in an eye with this configuration would be achieved by correcting the eye with a negative-power lens, which would shift the paraxial focus area back onto the retina.
-DOF (Depth of Focus): The range over which the caustic generates an acceptable level of blur.
-U DOF (Useful Depth of Focus): The portion of the DOF located in front of the retinal plane, contributing effectively to the extension of near focus.
To address this, some EDOF optics are characterized by an abrupt transition between a small-diameter central myopizing zone and a concentric, more emmetropic annular zone, aimed at improving retinal imaging of distant targets for small pupil diameters. A small pupil diameter, by reducing the diameter of the defocus blur circle, enables slight myopic refraction to be advantageous. From this perspective, it would be fundamental to optimize the degree of central myopization based on the anticipated pupil diameter for postoperative distance vision.
A note on Presby-LASIK procedures
Increasing the prolate asphericity of the corneal profile is a commonly used strategy in presbyopic refractive surgery. Early European pioneers initially believed—correctly—that this would increase negative spherical aberration, thereby providing the operated eye with greater depth of field. However, if this strategy was implemented without further adjustments to correct ametropia (aiming for emmetropia), it was often unsuccessful, as a hyperopic shift was observed postoperatively. To address this, compensation nomograms were introduced, ultimately leading to an additional +2D in spherical equivalent correction to allow sufficient near vision without the need for glasses.
In the early stages, surgeons assumed that inducing negative spherical aberration alone would enhance the depth of field. However, they didn’t fully appreciate the need for central overcorrection, or « central myopization, » as this page explains. Negative spherical aberration (NSA) represents a gradient of vergence; it doesn’t simply provide near vision in an eye corrected for distance but rather supports distance vision in an eye corrected for near.
If we were content to make his cornea more prolate (dashed line) without modifying the central cornea, it would serve no purpose or even aggravate the situation by inducing hyperopia of peripheral rays (as the reduced local corneal curvature reduces the incidence angle). Inducing a more prolate asphericity without changing the corneal power fails to improve near vision.
By adjusting the Q-factor towards a more prolate value, a Seidel-type spherical aberration is induced, as the paraxial curvature of the cornea remains unchanged while the peripheral cornea flattens. To achieve a useful depth of focus, paraxial myopization is required. In theory, a treatment based on the induction of Zernike-type negative spherical aberration could more directly achieve this effect since Zernike negative spherical aberration combines both negative Seidel-type spherical aberration and positive defocus (inducing myopia).
This approach highlights that increasing negative spherical aberration alone is insufficient to provide adequate depth of field for presbyopia correction without an accompanying central myopization. This myopic shift ensures that the eye can achieve functional near vision, while the gradient of vergence from NSA extends distance clarity in eyes corrected primarily for near tasks.
Our experience with multifocal presbyopia correction techniques suggests that uncorrected near vision can be achieved with an equivalent of a negative spherical aberration coefficient (Zernike) at least equal to -0.2 microns for a 6 mm diameter, if and only if combined with a central myopic refraction of around 2 D in spectacle plane terms.
Given that such a modulation of vergence with a Zernike spherical aberration (SA) of -0.2 microns for a 6 mm diameter theoretically produces a central myopic shift of 1 D, the additional myopia induced beyond that contained within the Zernike SA is approximately 1 D. The use of Zernike modes in this domain indeed adds confusion and complexity to the planning.
The READ technique that I developed for the EX 500 laser (Alcon/Wavelight) is based on a more direct approach, which simplifies programming.
Unlike the monovision technique, where the entire pupil exhibits a myopic refraction, all presbyLASIK techniques using negative SA rely on partial central myopization. Negative spherical aberration enhances intermediate and distance vision by gradually reducing the central excess power towards the periphery of the pupil.
Here is an example of total ocular vergence maps measured in patients who underwent presbyLASIK, using various laser equipment and correction algorithms on the non-dominant eye (intended for near vision):
Despite the use of marketing-friendly terminology, most approaches are fundamentally based on the same principle. As the vergence maps illustrate, these methods share the characteristic of inducing central myopization combined with peripheral demyopization. This configuration aims to enhance the distance vision of the non-dominant eye and minimize the disparity with the dominant eye. Interestingly, these maps are rarely—if ever—presented by the proponents of these techniques, who, it must be said, are quick to tout their ‘secret recipes’ to promote their methods.
Improved Characterization of SA’s Impact on Ocular Multifocality
It is unfortunate that the application of a standard designed for instrumental optics (Zernike modes), applied by default in ophthalmology, has introduced such confusion. To address this, we developed a new basis of high-degree polynomial functions (LD/HD) designed to interfere as minimally as possible with spherical-cylindrical refraction (second-order aberrations). These modes lack low-order terms, and in the context of our study on SA, we highlight that the corresponding mode (G40), like its Seidel counterpart, lacks any low-order terms:
G40(r) = √5 r4
Below is the wavefront error and vergence representation of this mode for a coefficient of 2 microns and a 6 mm pupil.
Using this mode more accurately reflects the impact of SA, which involves a vergence variation between the center (where it is negligible) and the edges of the pupil. This mode is certainly more neutral (although not completely, especially for large pupil diameters) than the Zernike mode with respect to spherical-cylindrical refraction. It can thus be understood as the gradient of central demyopization to be induced to optimize the performance of an operated eye when aiming for a certain degree of central myopization to extend the depth of focus towards distance vision.
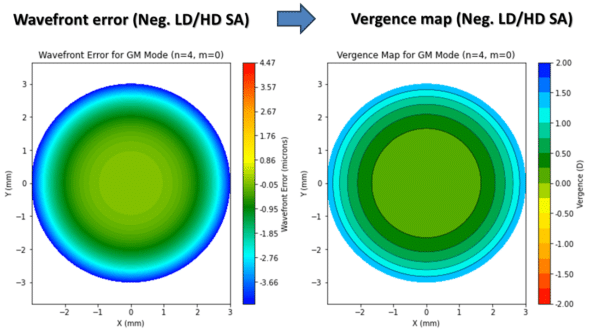
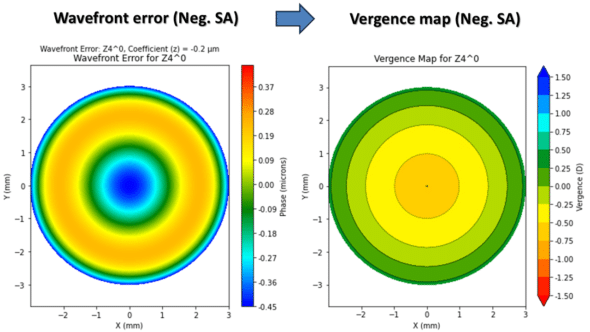
On the left is a wavefront error map corresponding to -2 microns of spherical aberration of the LD/HD type. On the right, the map of correpsonant vergence shows a gradient of about 2 D of hyperopia (central emmetropia, and hyperopia towards the edges of the pupil). This aberration, pure in higher-order terms, does not induce any significant variation in paracentral refraction.
Conclusion
In conclusion, a solid understanding of the theoretical foundations of optical aberrations—particularly negative spherical aberration (NSA)—is crucial for effectively applying these concepts in clinical settings. As the management of presbyopia increasingly incorporates controlled optical aberrations to extend depth of focus, comprehending the underlying mechanisms becomes essential. NSA, widely used in presbyLASIK and EDOF IOLs, offers significant potential for enhancing vision across varying distances, but only if applied with a precise awareness of its effects on vergence and image quality across the pupil.
It is essential to clearly understand the type of spherical aberration being referenced when a study or a promoter discusses its use for presbyopia compensation. Different types of spherical aberration, such as Seidel or Zernike, have distinct optical effects and implications. Misunderstanding the specific type can lead to incorrect assumptions about the expected clinical outcomes, making it crucial for practitioners to recognize which form of spherical aberration is being applied in each context.
This page aims to demystify the optical and refractive implications of Negative SA, illustrating how theoretical principles translate into clinical practice. By bridging these foundational concepts with practical application, ophthalmologists can better tailor their approach to presbyopic correction, balancing the trade-offs between distance clarity and extended near focus. Ultimately, such a nuanced understanding supports the development of optimized, patient-specific strategies that maximize visual outcomes in refractive and cataract surgery.
Related content and useful references
Numerous studies have explored the impact of spherical aberration on visual quality, spherical-cylindrical refraction, and depth of field. I encourage you to consult these resources if you’re curious and wish to delve deeper into this important field.
The following parameters have been taken into consideration in some studies:
- The influence of individual pupil dynamics in each eye
- The metrics employed (Strehl ratio, convolved images, MTF, etc.)
- The range of spatial frequencies considered
- The « Crawford effect » (attenuation of peripheral rays’ impact)
- Biometric characteristics (e.g., the influence of anterior chamber depth in pseudophakic eyes)
Can you recommend ‘hyper prolate contact lens?
Currently using aquacomfort multifocal hi center near, adjusting my script so peripheral power = my refracted power. As per a paper it has steep power profile all the way to edge
What’s difference between center near flat central with steep periphery vs steep central and flat periphery?
√5 * (6r4 – 6r2 + 1) is not equal to √5 * (6r4) – √15*√3(2r2 – 1)
What are the complications of BVI Isopure IOL?